Șiruri de numere reale
Orice funcție ![]() se numește șir de numere reale (link).
se numește șir de numere reale (link).
Aspecte referitoarea la reprezentarea grafică a unui șir de numere reale pot fi găsite aici.
Șirul ![]() este crescător dacă
este crescător dacă ![]() pentru orice
pentru orice ![]() .
.
Șirul ![]() este strict crescător dacă
este strict crescător dacă ![]() pentru orice
pentru orice ![]() .
.
Șirul ![]() este descrescător dacă
este descrescător dacă ![]() pentru orice
pentru orice ![]() .
.
Șirul ![]() este strict descrescător dacă
este strict descrescător dacă ![]() pentru orice
pentru orice ![]() .
.
Oricare din cele patru tipuri de șiruri definite mai sus este un șir monoton.
Teoremă
Șirul de numere reale ![]() are limita
are limita ![]() dacă și numai dacă în afara oricărei vecinătăți
dacă și numai dacă în afara oricărei vecinătăți ![]() rămâne un număr finit de termeni ai șirului.
rămâne un număr finit de termeni ai șirului.
Să se arate că șirul ![]() , cu termenul general
, cu termenul general ![]() pentru orice
pentru orice ![]() are limita
are limita ![]() .
.
Pentru orice ![]() , inegalitatea
, inegalitatea
![]()
implică ![]() sau, în mod echivalent,
sau, în mod echivalent,
(1) ![]()
În inegalitatea de mai sus se presupune cunoscută valoarea lui ![]() , deci trebuie determinată mulțimea valorilor admisibile ale lui
, deci trebuie determinată mulțimea valorilor admisibile ale lui ![]() . Atunci, rescriem inegalitatea sub forma
. Atunci, rescriem inegalitatea sub forma
![]()
ceea ce este echivalent cu
(2) ![]()
(3) ![]()
Calculul limitelor de șiruri conduce și la situații în care operațiile implicate sunt aparent imposibil de efectuat, așa numitele cazuri de nedeterminare. Acestea sunt

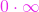

 – link
– link

Comentarii recente