Limita unui șir de numere reale

Pentru a consolida noțiunea de limită a unui șir de numere reale este indicat să se ilustreze definiția prin exemple concrete.

Spre exemplu, pentru șirul \left(a_n\right)_{n\ge 1}, cu termenul general a_n = \frac{n-1}{2n+1} pentru orice n\ge 1 , se poate arăta că are limita L=\frac{1}{2}.

Practic pentru orice \varepsilon >0, dacă se alege N(\varepsilon )=\left[ \frac{1}{2}\cdot \left( \frac{3}{2\varepsilon }-1\right) \right]+1, atunci \left| a_{n}-L\right| < \varepsilon pentru orice n \ge N(\varepsilon ).

Dacă se consideră \varepsilon =\frac{1}{10} se obține 

    \[N(\varepsilon )=% \left[ \frac{1}{2}\cdot \left( \frac{3}{2\cdot \frac{1}{10}}-1\right) \right] +1 %=\left[ \frac{1}{2}(15-1)\right] +1 =[7] =8.\]

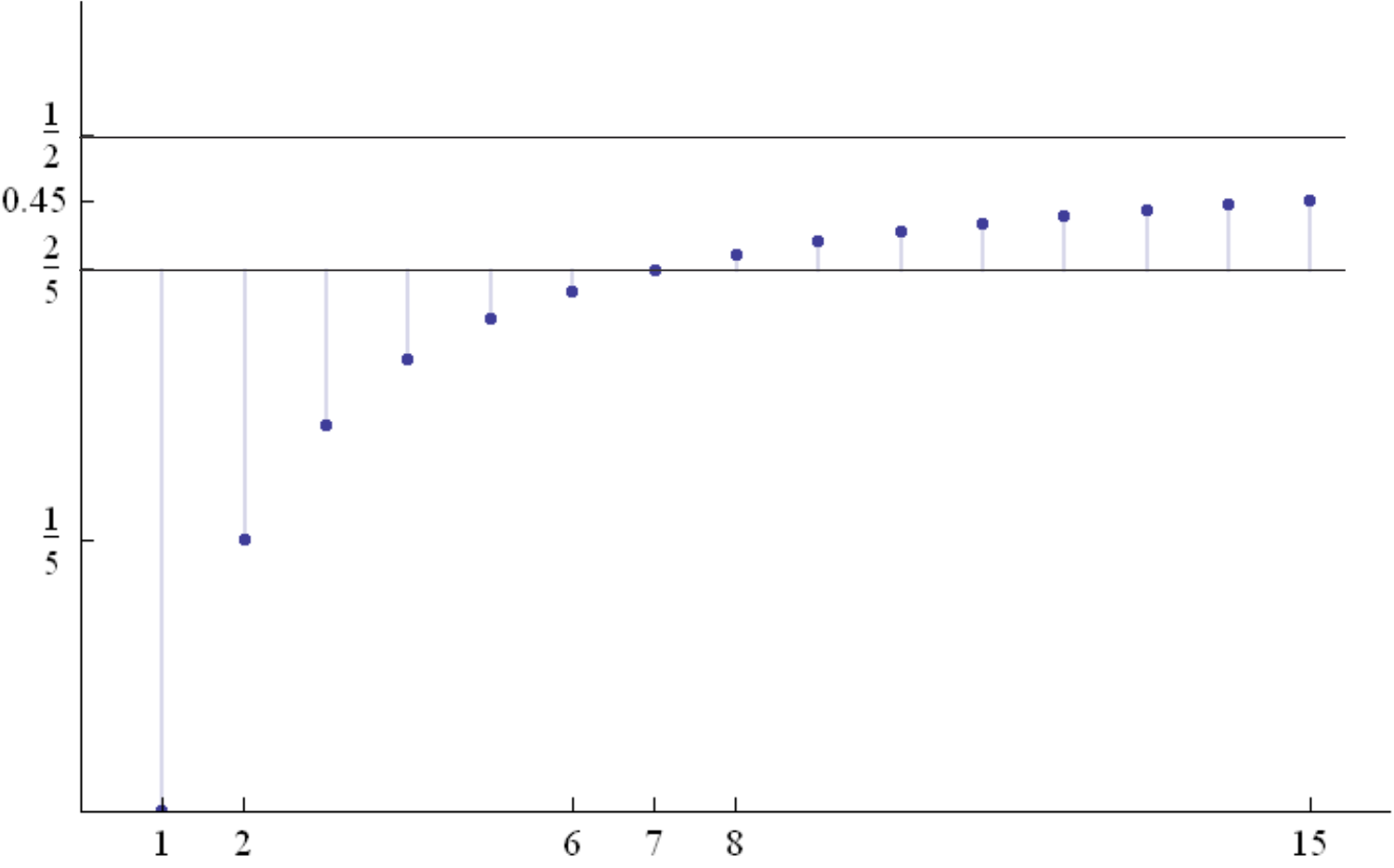
În figura de mai sus, se observă că primi șapte termeni ai șirului \left(\frac{n-1}{2n+1}\right)_{n\ge 1} nu se găsesc în intervalul V_\varepsilon = \left(L-\varepsilon, L+\varepsilon\right) = \left(\frac{2}{5}, \frac{3}{5}\right), iar toți ceilalți termeni aparțin intervalului \left(\frac{2}{5}, \frac{1}{2}\right) \subset V_\varepsilon.

Prin calcul direct se obține

    \begin{align*} a_6 &= \frac{5}{13} = \frac{25}{65} < \frac{26}{65} = \frac{2}{5} = L-\varepsilon, \\ a_7 &= \frac{2}{5} = L-\varepsilon, \\ a_8 &= \frac{7}{17} = \frac{35}{85} > \frac{34}{85} = \frac{2}{5} = L-\varepsilon. \end{align*}

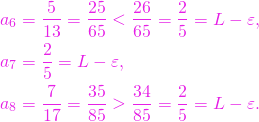
Monotonia șirului ne permite să considerăm că a_n \ge \frac{2}{5} oricare ar fi n \ge 8. Dar a_n < \frac{1}{2} oricare ar fi n\ge 1, deci o infinitate de termeni ai șirului \left(\frac{n-1}{2n+1}\right)_{n\ge 1} se găsesc în vecinătatea \left(\frac{2}{5}, \frac{1}{2}\right) a punctului L=\frac{1}{2}. Atunci

    \[\lim\limits_{n \to \infty} \frac{n-1}{2n+1} = \frac{1}{2}.\]