Calculul unei integrale Riemann
Enunț. Folosind definiția integralei Riemann, arătați că funcția ![]() ,
, ![]() este integrabilă Riemann pe intervalul
este integrabilă Riemann pe intervalul ![]() .
.
Soluție. Fie ![]()
![]() o diviziune a intervalui
o diviziune a intervalui ![]() și
și ![]() un sistem de puncte intermediare asociat diviziunii
un sistem de puncte intermediare asociat diviziunii ![]() . Suma Riemann atașată este
. Suma Riemann atașată este
![Rendered by QuickLaTeX.com \[ \sigma\left(f,\Delta,\xi\right) = \sum_{i=1}^{n} f\left(\xi_i\right) \cdot \left(x_i - x_{i-1}\right) = \sum_{i=1}^{n} \xi^2_i \cdot \left(x_i - x_{i-1}\right) . \]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-8554754b0ef263be2f6c2a88ab467153_l3.png)
Considerăm funcția ![]() ,
, ![]() pentru care se poate aplica Teorema lui Lagrange pe intervalul
pentru care se poate aplica Teorema lui Lagrange pe intervalul ![]() și se obține că pentru orice
și se obține că pentru orice ![]() există
există ![]() pentru care
pentru care
![]()
Atunci
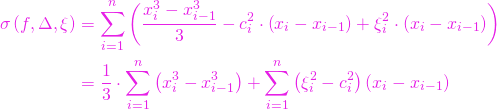
Cei doi termeni ai sumei de mai sus sunt evaluați independent. În primul rând
![Rendered by QuickLaTeX.com \[\frac{1}{3} \cdot \sum_{i=1}^{n} \left(x_i^3 - x_{i-1}^3\right) = \frac{b^3-a^3}{3},\]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-8d709717d1ec1f8795f379ded9bbe32d_l3.png)
iar în al doilea rând, cum funcția ![]() , dată de
, dată de ![]() este uniform continuă, avem că pentru orice
este uniform continuă, avem că pentru orice ![]() , există
, există ![]() astfel încât pentru orice
astfel încât pentru orice ![]() cu
cu ![]() are loc inegalitatea
are loc inegalitatea
![]()
Pentru ![]() avem
avem ![]() , deci
, deci
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{n} \left(\xi_i^2 - c_i^2 \right)\left(x_i - x_{i-1}\right) \le \frac{\varepsilon}{b-a} \cdot \sum_{i=1}^{n} \left(x_i - x_{i-1}\right) = \frac{\varepsilon}{b-a} \cdot \left(b-a\right) = \varepsilon. \]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-f2428fa16c162e9d05aefd7e00412d6d_l3.png)
Din cele de mai sus, putem spune că, pentru orice ![]() , există
, există ![]() astfel încât pentru orice
astfel încât pentru orice ![]() cu
cu ![]() avem
avem
![]()
ceea ce revine la faptul că
![]()
În concluzie, funcția ![]() ,
, ![]() este integrabilă Riemann pe intervalul
este integrabilă Riemann pe intervalul ![]() .
.
Enunț. Folosind suma Riemann atașată funcției ![]() ,
, ![]() , diviziunii echidistante a intervalului
, diviziunii echidistante a intervalului ![]() și sistemului de puncte intermediare cu punctele din capătul superior al fiecărui subinterval, calculați integrala Riemann a funcției
și sistemului de puncte intermediare cu punctele din capătul superior al fiecărui subinterval, calculați integrala Riemann a funcției ![]() .
.
Soluție.
Cu alegerea indicată se obține suma Riemann (pentru detalii vezi link)
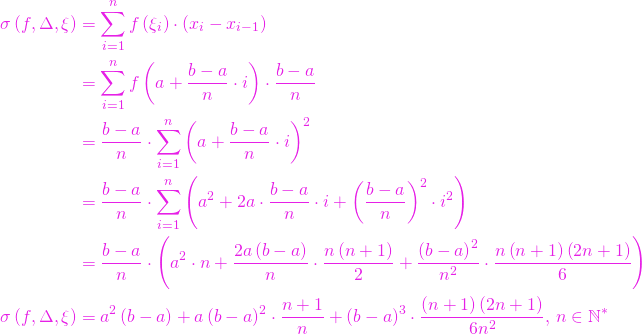
Atunci
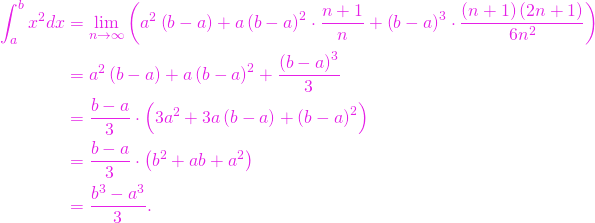
Alte exemple pot fi găsite în lucrarea
M. Roșculeț et. al., Probleme de analiză matematică, Ed. Tehnică, București, 1993

Comentarii recente