AM1-Curs-01
Mulțimi și relații
Teoria mulţimilor este creaţia genială a matematicianului Georg Cantor.
Noţiunea de mulţime este o noţiune primară care trebuie acceptată ca fiind o colecţie de obiecte, numite elemente, având o caracteristică comună.
O mulţime poate fi dată (definită) prin enumerarea elementelor sale sau prin precizarea unei proprietăţi comune ![]() a elementelor sale
a elementelor sale
![]()
Dacă ![]() este un element al mulțimii
este un element al mulțimii ![]() , atunci scriem
, atunci scriem ![]() , iar dacă
, iar dacă ![]() nu este element al mulțimii
nu este element al mulțimii ![]() atunci scriem
atunci scriem ![]() .
.
Definiţia 1.1. Mulțimea ![]() este inclusă în mulțimea
este inclusă în mulțimea ![]() dacă toate elementele mulțimii
dacă toate elementele mulțimii ![]() sunt elemente ale mulțimii
sunt elemente ale mulțimii ![]() , adică
, adică
![]()
Definiția 1.2. Fie ![]() și
și ![]() două mulțimi nevide și
două mulțimi nevide și ![]() cu
cu ![]() . Tripletul
. Tripletul ![]() se numește relație binară între mulțimile
se numește relație binară între mulțimile ![]() și
și ![]() . Dacă
. Dacă ![]() , spunem că elementul
, spunem că elementul ![]() se află în relația
se află în relația ![]() cu elementul
cu elementul ![]() și scriem
și scriem ![]() , dacă
, dacă ![]() .
.
Mulțimea
![]()
se numește domeniul relației ![]() , iar mulțimea
, iar mulțimea
![]()
se numește codomeniul relației ![]() .
.
Definiția 1.3. Fie ![]() o relație binară între mulțimile
o relație binară între mulțimile ![]() și
și ![]() , cu domeniul
, cu domeniul ![]() și codomeniul
și codomeniul ![]() . Dacă
. Dacă ![]() , se numește tăietură (secțiune) a relației
, se numește tăietură (secțiune) a relației ![]() prin elementul
prin elementul ![]() , mulțimea
, mulțimea
![]()
Definiția 1.4. Spunem că relația ![]() este univocă dacă pentru orice
este univocă dacă pentru orice ![]() , tăietura
, tăietura ![]() conține un singur element
conține un singur element ![]() , adică există o singură pereche
, adică există o singură pereche ![]() pentru fiecare
pentru fiecare ![]() . În caz contrar, adică dacă există
. În caz contrar, adică dacă există ![]() astfel încât tăietura
astfel încât tăietura ![]() să conțină mai multe elemente
să conțină mai multe elemente ![]() , atunci spunem că relația
, atunci spunem că relația ![]() este multivocă.
este multivocă.
Definiția 1.5. Relația binară ![]() se numește relație peste tot definită dacă domeniul relației
se numește relație peste tot definită dacă domeniul relației ![]() coincide cu
coincide cu ![]() , adică
, adică ![]() .
.
Definiția 1.6. Fie ![]() și
și ![]() două mulțimi nevide și
două mulțimi nevide și ![]() . Relația binară
. Relația binară ![]() între mulțimile
între mulțimile ![]() și
și ![]() se numește relație funcțională (sau funcție sau aplicație) dacă ea este univocă și peste tot definită, adică
se numește relație funcțională (sau funcție sau aplicație) dacă ea este univocă și peste tot definită, adică
![]()
Elementul ![]() se notează
se notează ![]() și se numește valoarea funcției
și se numește valoarea funcției ![]() în punctul
în punctul ![]() .
.
Exemple de funcții pot fi găsite la link1, link2.
Mulțimea numerelor reale
Există mai multe construcții ale mulțimii numerelor reale.
Axiomele mulțimii numerelor reale
Există trei grupe de axiome care definiesc mulțimea numerelor reale.
Axiomele structurii algebrice ale lui 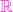
În mulțimea ![]() sunt definite două operații algebrice interne:
sunt definite două operații algebrice interne:
- adunarea
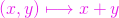
- înmulțirea
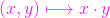 .
.
Tripletul ![]() este un corp comutativ.
este un corp comutativ.
Cu alte cuvinte, au loc următoarele proprietăți:
(1![]() ) Asociativitatea adunării
) Asociativitatea adunării
![]()
(2![]() ) Comutativitatea adunării
) Comutativitatea adunării
![]()
(3![]() ) Existența elementului neutru pentru operația de adunare
) Existența elementului neutru pentru operația de adunare
![]()
(4![]() ) Existența elementelor simetrizabile pentru operația de adunare
) Existența elementelor simetrizabile pentru operația de adunare
![]()
(5![]() ) Asociativitatea înmulțirii
) Asociativitatea înmulțirii
![]()
(6![]() ) Comutativitatea înmulțirii
) Comutativitatea înmulțirii
![]()
(7![]() ) Existența elementului neutru pentru operația de înmulțire
) Existența elementului neutru pentru operația de înmulțire
![]()
(8![]() ) Existența elementelor simetrizabile pentru operația de înmulțire
) Existența elementelor simetrizabile pentru operația de înmulțire
![]()
(9) Distributivitatea înmulțirii față de adunare
![]()
Axiomele de ordine din mulțimea 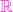
(10) Reflexivitatea
![]()
(11) Tranzitivitatea
![]()
(12) Antisimetria
![]()
(13) Relația de ordine este totală
![]()
(14) Compatibilitatea relației de ordine cu adunarea
![]()
(15) Compatibilitatea relației de ordine cu înmulțirea
![]()
Axioma marginii superioare (axioma Cantor–Dedekind)
Pentru orice submulțime nevidă majorată ![]() , există marginea superioară
, există marginea superioară ![]() .
.
Tema se găsește la acest link.

Comentarii recente