Nedeterminarea 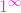
Cazul de nedeterminare ![]() se poate rezolva prin aplicarea următorului rezultat
se poate rezolva prin aplicarea următorului rezultat
Dacă șirul 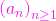 este astfel încât
este astfel încât 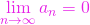 , atunci
, atunci
![]()
Exercițiu rezolvat
Să se calculeze următoarea limită
![]()
Rezolvare.
Cum șirul ![]() este convergent către
este convergent către ![]() , atunci se observă că inițial avem nedeterminarea
, atunci se observă că inițial avem nedeterminarea ![]() .
.
Pentru început determinăm termenul general al șirului ![]() , cu
, cu ![]() . Avem
. Avem
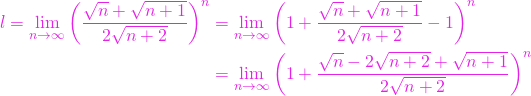
Deci ![]() oricare ar fi
oricare ar fi ![]() .
.
Aplicăm rezultatul de mai sus și se obține
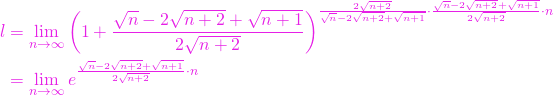
În continuare, calculăm limita de la exponent
![]()
unde avem cazul de nedeterminare ![]() .
.
Efectuăm următorii pași:
1. raționalizăm termenul din mijloc
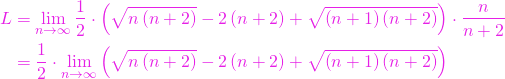
2. descompunem suma în doi termeni
![]()
3. raționalizăm fiecare termen și finalizăm calculele
![Rendered by QuickLaTeX.com \begin{align*} L& = \frac{1}{2} \cdot \left[ \lim\limits_{n\to\infty} \frac{n\left(n+2\right) - \left(n+2\right)^2}{\sqrt{n\left(n+2\right)} + \left(n+2\right)} + \lim\limits_{n\to\infty} \frac{\left(n+1\right)\left(n+2\right) - \left(n+2\right)^2}{\sqrt{\left(n+1\right)\left(n+2\right)} + \left(n+2\right)}\right]\\ & =\frac{1}{2} \cdot \left[ \lim\limits_{n\to\infty} \frac{-2n-4}{\sqrt{n\left(n+2\right)} + \left(n+2\right)} + \lim\limits_{n\to\infty} \frac{-n-2}{\sqrt{\left(n+1\right)\left(n+2\right)} + \left(n+2\right)} \right] \\ & = \frac{1}{2} \cdot \left(-1 - \frac{1}{2}\right) \\ & = - \frac{3}{4} \end{align*}](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-5761f4354f4df88259a6c60fa365fad5_l3.png)
Atunci
![]()

Comentarii recente