AM1-Curs-05

Serii de numere reale

 

Fie (u_n) un șir de numere reale. Suma inifinită

    \[\sum\limits_{n=1}^\infty u_n\]

se numește serie de numere reale atașată șirului \left( u_n \right)_{n\ge 1}.

Fiind dată seria \sum\limits_{n=1}^\infty u_n, șirul cu termenul general

    \[s_n = \sum\limits_{k=1}^n u_k = u_1 + u_2 + \ldots + u_n, n\ge 1\]

se numește șirul sumelor parțiale.

Fie seria de numere reale \sum\limits_{n=1}^\infty u_n. Spunem că seria este convergentă, dacă șirul sumelor parțiale (s_n) este un șir convergent în \mathbb{R} și spunem că seria este divergentă dacă șirul sumelor parțiale (s_n) este divergent în \mathbb{R}. Dacă \lim\limits_{n\to\infty} s_n=S \in \mathbb{R}, atunci S se numește suma seriei, adică

(1)   \begin{equation*} S=\lim\limits_{n\to\infty} (u_1 +u_2 +\ldots +u_n)=\sum\limits^\infty_{n=1} u_n \end{equation*}

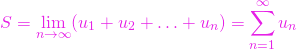
Dintre seriile remarcabile amintim aici seria armonică

    \[ \sum\limits_{n=1}^\infty \frac{1}{n} \]

precum și seria geometrică 

    \[ \sum\limits_{n=1}^\infty q^{n} , \, q \in \mathbb{R}. \]

Observație. Pentru |q| < 1 seria geometrică \sum\limits_{n=1}^\infty q^{n} este convergentă și are suma S=\frac{q}{1-q}.

Exercițiu. Să se calculeze suma seriei

    \[ \sum\limits_{n=1}^\infty \frac{1}{4n^2+8n+3}\]

Soluție.

Criterii de convergență pentru serii de numere reale pot fi găsite aici.