AM2-Curs-01
Șiruri de puncte din 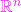
Definiție
Se numește șir de puncte din ![]() orice funcție
orice funcție ![]() .
.
Un șir de puncte din ![]() se va nota prescurtat
se va nota prescurtat ![]() , unde
, unde
![]() cu
cu ![]() .
.
Definiție
Punctul ![]() este limita șirului
este limita șirului ![]() dacă în afara oricărei vecinătăți a punctului
dacă în afara oricărei vecinătăți a punctului ![]() se găsesc cel mult un număr finit de termeni ai șirului. În acest caz se utilizează notația
se găsesc cel mult un număr finit de termeni ai șirului. În acest caz se utilizează notația
(1) ![]()
Teorema Fie ![]() un șir de puncte din
un șir de puncte din ![]() și
și ![]() . Atunci
. Atunci
![]()
![]()
Un șir din ![]() este convergent dacă are limită finită.
este convergent dacă are limită finită.
Teorema Limita unui șir convergent din ![]() este unic determinată.
este unic determinată.
Teorema Fie ![]() ,
, ![]() și
și ![]() . Dacă
. Dacă
-
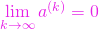 ,
, - există
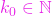 astfel ca
astfel ca 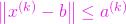 ,
,  ,
, 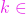 ,
,
atunci
![]()
Teorema Fie ![]() , și
, și ![]() . Dacă
. Dacă ![]() , atunci
, atunci
(2) ![]()
Teorema Dacă șirul ![]() este convergent, atunci
este convergent, atunci ![]() este și mărginit, adică există
este și mărginit, adică există ![]() astfel încât
astfel încât
(3) ![]()
Definiție
Șirul ![]() se numește șir fundamental sau șir Cauchy, dacă
se numește șir fundamental sau șir Cauchy, dacă
(4) ![]()
(5) ![]()
Teorema
Șirul ![]() este convergent dacă și numai dacă este fundamental.
este convergent dacă și numai dacă este fundamental.
Teorema
Fie ![]() , cu
, cu ![]() și
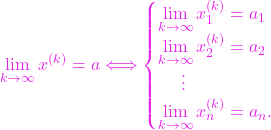
și ![]() . Atunci
. Atunci
(6) 

Comentarii recente