AM2-Curs-02
Funcţii de variabilă vectorială cu valori vectoriale
Fie ![]() două numere naturale nenule. Funcţia
două numere naturale nenule. Funcţia ![]() se numeşte funcţie vectorială sau funcţie de variabilă vectorială cu valori vectoriale, unde
se numeşte funcţie vectorială sau funcţie de variabilă vectorială cu valori vectoriale, unde
![]()
Dacă ![]() , atunci avem o funcţie reală
, atunci avem o funcţie reală
![]()
Dacă ![]() şi
şi ![]() , atunci avem o funcţie vectorială cu valori reale
, atunci avem o funcţie vectorială cu valori reale
![]()
Dacă ![]() şi
şi ![]() , atunci avem o funcţie reală cu valori vectoriale
, atunci avem o funcţie reală cu valori vectoriale
![]()
Limita unei funcții într-un punct
Fie ![]() un punct de acumulare al mulțimii
un punct de acumulare al mulțimii ![]() . Punctul
. Punctul ![]() este limita funcției
este limita funcției ![]() în punctul
în punctul ![]() dacă și numai dacă pentru orice vecinătate
dacă și numai dacă pentru orice vecinătate ![]() a punctului
a punctului ![]() există o vecinătate
există o vecinătate ![]() a punctului
a punctului ![]() astfel încât oricare ar fi
astfel încât oricare ar fi ![]() ,
, ![]() avem
avem ![]() .
.
Se utilizează notația
![]()
Limite parţiale
Fie ![]() . Presupunem că
. Presupunem că ![]() , unde
, unde ![]() ,
, ![]() , cu
, cu ![]() .
.
Fie ![]() , cu
, cu ![]() şi
şi ![]() şi
şi
![]()
Facem notaţia ![]() .
.
Dacă pentru ![]() fixat există limita
fixat există limita
![]()
atunci ![]() se numeşte limita parţială a funcţiei
se numeşte limita parţială a funcţiei ![]() în raport cu
în raport cu ![]() în punctul
în punctul ![]() .
.
Dacă pentru ![]() , fixat, există limita
, fixat, există limita
![]()
atunci ![]() se numeşte limita parţială a funcţiei
se numeşte limita parţială a funcţiei ![]() în raport cu
în raport cu ![]() în punctul
în punctul ![]() .
.
Dacă există limitele parţiale
![]()
![]()
atunci ele se numesc limitele iterate ale funcţiei ![]() în punctul
în punctul ![]() . Dacă mai există şi limita funcţiei
. Dacă mai există şi limita funcţiei ![]() în punctul
în punctul ![]() , adică
, adică
![]()
atunci această limită se numeşte limita globală a funcţiei ![]() în punctul
în punctul ![]() .
.
Funcție continuă
Definiție. Fie ![]() o aplicație. Spunem că
o aplicație. Spunem că ![]() este continuă în punctul
este continuă în punctul ![]() , dacă
, dacă
![]()
Are loc următorul rezultat de caracterizare a continuității într-un punct.
Teoremă. Fie ![]() o aplicație și
o aplicație și ![]() , atunci următoarele afirmații sunt echivalente:
, atunci următoarele afirmații sunt echivalente:
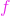 este continuă în punctul
este continuă în punctul  ,
,- oricare ar fi
 există
există  ,
,
![Rendered by QuickLaTeX.com \[ \forall x\in D, \left\| x - a \right\| < \delta_\varepsilon, \Rightarrow \left\| f\left(x\right) - f\left(a\right) \right\| <\varepsilon. \]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-eb2214f046e5cbed8e9335341cf93941_l3.png)
- oricum am alege un șir
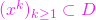 cu
cu 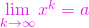 avem
avem
![Rendered by QuickLaTeX.com \[\lim\limits_{k \to \infty} f\left(x^k\right) = f\left(a\right) .\]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-8209ea19a452ef576f050acec7e23d14_l3.png)
Are loc următorul rezultat de caracterizare a continuității globale.
Teoremă. Fie ![]() o aplicație, atunci următoarele afirmații sunt echivalente:
o aplicație, atunci următoarele afirmații sunt echivalente:
- funcția
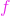 este continuă pe mulțimea
este continuă pe mulțimea  ,
, - pentru orice submulțime
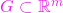 deschisă, mulțimea
deschisă, mulțimea 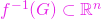 este deschisă,
este deschisă, - pentru orice submulțime
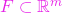 închisă, mulțimea
închisă, mulțimea 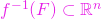 este închisă.
este închisă.
Reamintesc că mulțimea
![]()
este imaginea inversă a mulțimii ![]() prin funcția
prin funcția ![]() .
.

Comentarii recente