AM2-Tema-3

Aici veți găsi o listă cu exerciții care necesită cunoștințe referitoare la noțiunea de derivată parțială a unei funcții de două sau trei variabile reale cu valori reale.

Exercițiul 1. Determinați derivatele parțiale ale următoarelor funcții:

$f:\mathbb{R}^2\to \mathbb{R}$ , $f(x,y)=4x^2-2x^2 y+5y^2-2x+xy+1$ ;
$f:\mathbb{R}^2\setminus\left\{(x,y) |xy=0\right\}\to\mathbb{R}$ , $f(x,y)=x^2 y+\cfrac{x}{y}+\cfrac{y^2}{x}$ ;
$f:\mathbb{R}^2\to\mathbb{R}$ , $f(x,y)=x^2+xy+e^{-x^2 y}$ ;
$f:\left\{\left( x,y \right)\in \mathbb{R}^2, xy>0\right\} \to \mathbb{R}$ , $f\left( x,y \right) = \dfrac{1}{\sqrt{xy}} + \ln \dfrac{y}{x}$ ;
$f:\mathbb{R}^2 \to \mathbb{R}$ , $f\left( x,y \right) = \ln\left( x^2+y^2 +1 \right)$ .

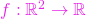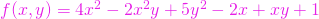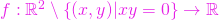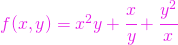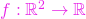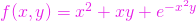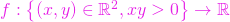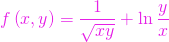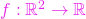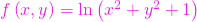Exercițiul 2. Fie funcția $f:\mathbb{R}^2\setminus\left\{\left( 0,0 \right) \right\} \to \mathbb{R}$ definită prin

$f\left( x,y \right) = \ln \left( x^2 + xy +y^2 \right).$

Arătați că

$x\frac{\partial f}{\partial x}\left( x,y \right) + y \frac{\partial f}{\partial y}\left( x,y \right) = 2$

oricare ar fi $\left( x,y \right) \in \mathbb{R}^2\setminus\left\{\left( 0,0 \right) \right\}$ .

Exercițiul 3. Arătați că derivatele parțiale ale funcției $F: D \to \mathbb{R}$ , $F \left(x,y,z\right) = \ln \left(x^3 + y^3 + z^3 - 3xyz\right)$ , unde $D=\left\{ \left(x,y,z\right) \in \mathbb{R} | \, x^3 + y^3 + z^3 - 3xyz > 0\right\}$ , satisfac relația

$\frac{\partial F}{\partial x} \left(x,y,z\right) + \frac{\partial F}{\partial y} \left(x,y,z\right) + \frac{\partial F}{\partial z} \left(x,y,z\right) = \frac{3}{x+y+z}.$

Exercițiul 4. Fie funcția $f:\mathbb{R}^2 \to \mathbb{R}$ definită prin

$f\left(x,y\right) = \begin{cases} xy\cdot \frac{x^2-y^2}{x^2+y^2}, \text{ dac\u a } \left(x,y\right)\ne \left(0,0\right) \\ 0 \text{ dac\u a } \left(x,y\right)\ne \left(0,0\right). \end{cases}$