Ex-AM2-Curs-04
Exercițiu. Studiați diferențiabilitatea în punctul ![]() a funcției
a funcției ![]() definită prin
definită prin
![Rendered by QuickLaTeX.com \[f\left(x,y\right) = \begin{cases} \left(x^2 + y^2\right) \sin \dfrac{1}{x^2 + y^2}, \enskip \left(x,y\right) \ne \left(0,0\right) \\ 0, \enskip \left(x,y\right) = \left(0,0\right)\end{cases}.\]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-a334d34a3048d945e0b0bac1329636c4_l3.png)
Soluție
Pentru început verificăm dacă funcția ![]() este derivabilă parțial în punctul
este derivabilă parțial în punctul ![]() .
.
Avem
![]()
![]()
Deci ![]() este derivabilă parțial în punctul
este derivabilă parțial în punctul ![]() .
.
Considerăm funcția ![]() definită prin
definită prin
![Rendered by QuickLaTeX.com \[ \omega\left(x,y\right) = \begin{cases} \dfrac{f\left(x,y\right) - f\left(0,0\right) - x\cdot\diffp{f}{x}\left(0,0\right) - y \cdot \diffp{f}{y}\left(0,0\right)}{\sqrt{x^2 + y^2}}, \enskip \left(x,y\right) \ne \left(0,0\right) \\ 0, \enskip \left(x,y\right) = \left(0,0\right), \end{cases} \]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-6885db2e30f37469fe1171606f3bd40d_l3.png)
adică
![Rendered by QuickLaTeX.com \[\omega\left(x,y\right) = \begin{cases} \sqrt{x^2 + y^2} \cdot \sin \dfrac{1}{x^2 + y^2}, \enskip \left(x,y\right) \in \left(0,0\right) \\ 0,\enskip \left(x,y\right) = \left(0,0\right).\end{cases}\]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-9c69f8d90170f6681ad9536d5236eb6b_l3.png)
Studiem continuitatea funcției ![]() în punctul
în punctul ![]() . Fie
. Fie ![]() un șir de numere reale cu
un șir de numere reale cu ![]() . Cum
. Cum
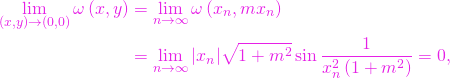
oricare ar fi ![]() , obținem că
, obținem că ![]() este continuă în punctul
este continuă în punctul ![]() .
.
Atunci ![]() este diferențiabilă în punctul
este diferențiabilă în punctul ![]() .
.

Comentarii recente