AM2-Curs-05
Extremele locale ale unei funcții reale de mai multe variabile reale
Fie ![]() și funcția
și funcția ![]() . Punctul
. Punctul ![]() se numește punct de minim local al funcției
se numește punct de minim local al funcției ![]() , dacă există
, dacă există ![]() astfel încât
astfel încât
(1) ![]()
punctul
(2) ![]()
Numărul
Dacă inegalitatea (1) sau (2) are loc pentru orice ![]() , atunci spunem că
, atunci spunem că ![]() este un punct de optim global.
este un punct de optim global.
Definiție. Fie ![]() ,
, ![]() și
și ![]() , o funcție diferențiabilă în punctul
, o funcție diferențiabilă în punctul ![]() . Dacă
. Dacă ![]() sau
sau ![]() , atunci spunem că
, atunci spunem că ![]() este punct staționar (sau punct critic) al funcției
este punct staționar (sau punct critic) al funcției ![]() .
.
Teoremă. Fie ![]() o mulțime deschisă și convexă,
o mulțime deschisă și convexă, ![]() o funcție de clasă
o funcție de clasă ![]() și
și ![]() un punct critic al funcției
un punct critic al funcției ![]() . Atunci
. Atunci
- dacă
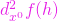 este o formă pătratică pozitiv definită, atunci
este o formă pătratică pozitiv definită, atunci 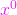 este un punct de minim local al funcției
este un punct de minim local al funcției 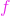 ,
, - dacă
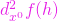 este negativ definită, atunci
este negativ definită, atunci 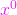 este un punct de maxim local al funcției
este un punct de maxim local al funcției 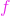 ,
, - dacă
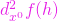 este o formă pătratică nedefinită, atunci
este o formă pătratică nedefinită, atunci 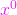 nu este un punct de optim local al funcției
nu este un punct de optim local al funcției 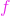 .
.
Pentru următorul rezultat vom folosi notația
![]()
(3) 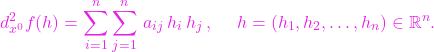
Teoremă. Fie ![]() o mulțime deschisă,
o mulțime deschisă, ![]() un punct critic al funcției
un punct critic al funcției ![]() , unde
, unde ![]() este o funcție de clasă
este o funcție de clasă ![]() . Atunci
. Atunci
- Dacă
![Rendered by QuickLaTeX.com \[\Delta_1=a_{11}>0,\;\Delta_2=\left|\begin{array}{ll} a_{11} & a_{12}\\[5pt] a_{21} & a_{22} \end{array}\right|>0,\dots,\Delta_n=\left| \begin{array}{llll} a_{11} & a_{12} & \dots & a_{1n}\\[5pt] a_{21} & a_{22} & \dots & a_{2n}\\[5pt] \cdot & \cdot & \dots & \cdot \\[5pt] a_{n1} & a_{n2} & \dots & a_{nn} \end{array}\right|>0\,,\]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-6c209c8f51c5cb05241e7084fc84aa90_l3.png)
atunci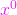 este un punct de minim local al funcției
este un punct de minim local al funcției 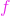 .
. - Dacă
![Rendered by QuickLaTeX.com \[\Delta_1=a_{11}<0,\quad\Delta_2=\left| \begin{array}{ll} a_{11} & a_{12}\\[5pt] a_{21} & a_{22} \end{array}\right|>0,\quad\Delta_3<0,\dots,(-1)^n\Delta_n>0\,,\]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-49fd67be8706100cea0ca191e6b35064_l3.png)
atunci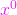 este un punct de maxim local al funcției
este un punct de maxim local al funcției 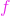 .
.
Un exemplu de aplicare a acestui rezultat poate fi consultat aici.
Partea a doua a acestui curs poate fi consultată aici.
Pentru a studia reprezentarea grafică a unor funcții de două variabile puteți folosi CalcPlot3D.

Comentarii recente