O sumă Riemann
Enunț. Determinaţi suma Riemann ataşată funcţiei ![]() ,
, ![]() , diviziunii echidistante cu
, diviziunii echidistante cu ![]() noduri a intervalului
noduri a intervalului ![]() şi sistemului de puncte intermediare
şi sistemului de puncte intermediare ![]() ,
, ![]() .
.
Cum diviziunea echidistantă are cele ![]() noduri ale intervalului
noduri ale intervalului ![]() date prin
date prin
![]()
se obţine
![]()
şi
![]()
Atunci, suma Rieman este
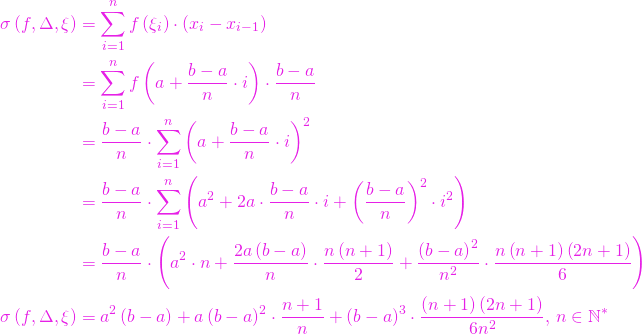

Comentarii recente