Funcții raționale simple
O funcție rațională ![]() se numește funcție rațională simplă sau fracție simplă dacă are una din următoarele forme:
se numește funcție rațională simplă sau fracție simplă dacă are una din următoarele forme:
I. ![]() cu
cu ![]() și
și ![]() ,
, ![]() ;
;
II. ![]() , unde
, unde ![]() ,
, ![]() ,
, ![]() ;
;
III. ![]() , unde
, unde ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() și
și ![]() .
.
Orice altă funcție rațională ![]() , este o combinație liniară de funcții raționale simple.
, este o combinație liniară de funcții raționale simple.
Teoremă. Fie funcția rațională ![]() , cu
, cu ![]() , unde
, unde ![]() și
și ![]() sunt polinoame cu coeficienți reali, prime între ele și
sunt polinoame cu coeficienți reali, prime între ele și ![]() . Dacă
. Dacă ![]() se descompune în factori ireductibili, adică
se descompune în factori ireductibili, adică
(1) ![]()
unde ![]() ,
, ![]() sunt rădăcinile reale ale polinomului
sunt rădăcinile reale ale polinomului ![]() , iar
, iar ![]() , pentru
, pentru
![]() și
și ![]() cu
cu
![]()
atunci există un polinom cu coeficienți reali ![]() , și constantele reale
, și constantele reale ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() astfel încât funcția
astfel încât funcția ![]() se scrie în mod unic sub forma
se scrie în mod unic sub forma
![Rendered by QuickLaTeX.com \[ f(x)=p(x)+\sum\limits_{i=1}^{k}\,\left( {\,}\frac{A_{i}^{1}}{x-x_{i}}+\frac{% A_{i}^{2}}{(x-x_{i})^{2}}+\ldots +\frac{A_{i}^{n_{i}}}{(x-x_{i})^{n_{i}}}% \,\right) + \]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-40fdd53d97f569a58dd9d21e39e8a2bc_l3.png)
(2) 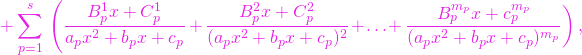
pentru orice ![]() .
.
Alte detalii pot fi găsite aici.

Comentarii recente