Tema 2b-AM2
am2c2p1 Studiați continuitatea funcției ![]() definită prin
definită prin
![]()
am2c2p2 Determinați mulțimea punctelor de discontinuitate pentru funcțiile
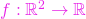 unde
unde
![Rendered by QuickLaTeX.com \[f\left(x,y\right) = \ln\left(x^2+y^2\right), \text{ dac\u a } x^2+y^2\ne 0 \]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-b747f1bf16ae332d7dcf68ada1df2105_l3.png)
și
![Rendered by QuickLaTeX.com \[f\left(x,y\right) = 0, \text{ dac\u a } x^2+y^2=0. \]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-ede988bdf647e6ca18192ab8f22b0b62_l3.png)
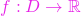 cu
cu 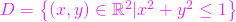 unde
unde
![Rendered by QuickLaTeX.com \[f\left(x,y\right) = \frac{1}{1-x^2-y^2}, \text{ dac\u a } x^2+y^2<1 \]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-ce659062bf69251901fb0b030ec1b2e9_l3.png)
și
![Rendered by QuickLaTeX.com \[f\left(x,y\right) = 0, \text{ dac\u a } x^2+y^2=1. \]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-ca4f6eac82243a9cbaf878b87ea02d80_l3.png)
am2c2p3 Arătați că funcția ![]() cu
cu
![Rendered by QuickLaTeX.com \[f\left(x,y\right) = \begin{cases} \frac{2xy}{x^2 + y^2} \text{ dac\u a } x^2+y^2 \ne 0 \\ 0 \text{ dac\u a } x=y=0 \end{cases} \]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-e43833b4e79bc4113fce16764d25ccf8_l3.png)
nu este continuă în punctul ![]() , dar funcțiile reale obținute prin considerarea unei variabile ca fiind o constantă reală fixată sunt funcții continue.
, dar funcțiile reale obținute prin considerarea unei variabile ca fiind o constantă reală fixată sunt funcții continue.

Comentarii recente