Metoda figurativă

Esențial la rezolvarea problemelor prin metoda figurativă este pasul numit egalarea părților. În continuare, am să evidențiez această etapă a rezolvării problemelor prin metoda figurativă, luând în considerare două cazuri particulare.

Cazul 1

Considerăm cazul problemelor în care se cere determinarea a două cantități atunci când se cunosc suma și diferența lor.

Din punct de vedere algebric, trebuie să rezolvăm sistemul de ecuații

    \[ \begin{cases} a+b= S \\ a-b = D\end{cases}\]

unde numerele S și D sunt cunoscute, iar a, b sunt necunoscutele. Soluția acestui sistem este

    \[ \begin{cases} a=\frac{1}{2}\cdot \left(S+D\right) \\ b=\frac{1}{2}\cdot \left(S-D\right) \end{cases}\]

Rezolvarea prin metoda figurativă poate fi organizată sub următoarea formă

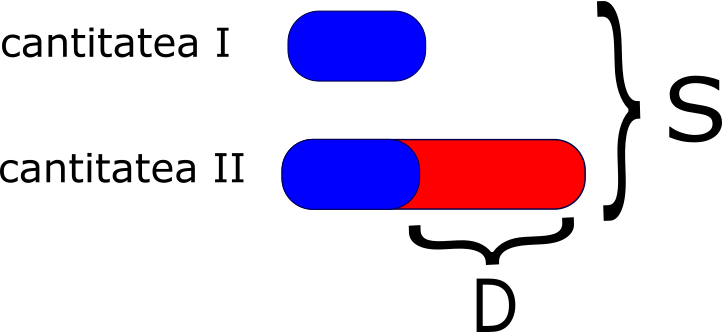
Se observă că apar două segmente egale (cele albastre), iar problema este să determinăm cantitatea pe care acestea o reprezintă.

Se ajunge la concluzia că cele două segmente egale reprezintă diferența dintre cele două cantități cunoscute. Astfel calculul

    \[\left(S-D\right):2\]

ne permite să determinăm valoare pe care o reprezintă segmentul unitate, adică numărul cel mai mic.

La următorul pas se determină cel de al doilea număr, ceea ce se poate realiza fie prin scăderea din suma S a numărului mic (cel care tocmai a fost determinat), fie prin adunarea la diferența D a numărului mic.

Cazul 2

Considerăm cazul problemelor în care se cunosc diverse valori ale rapoartelor a două cantități și se cere determinarea acestor cantități. Mai exact, ne referim la rezolvarea sistemului de ecuații

    \[ \begin{cases} \frac{a}{b} = p \\ \frac{a-n}{b-n} = q \end{cases} \]

unde numerele nenule n, p și q sunt cunoscute.

Soluția acestui sistem este

    \[\begin{cases} a=\frac{q-1}{q-p} \cdot pn \\ b=\frac{q-1}{q-p} \cdot n\end{cases}\]

Rezolvarea prin metoda figurativă necesită următoarele reprezentări.

Pentru început, cantitatea I, cantitate mai mică, notată cu b în sistemul precedent, se cuprinde de p ori în cantitatea a II-a, cea mai mare, notată cu a în sistemul de mai sus. Acest fapt este reprezentat în figura de mai jos

Cele două cantități se micșorează cu n și astfel cantitatea mai mică se cuprinde de q ori în cantitatea mai mare. Deci, segmentul albastru este format dintr-un nou segment, cel verde, și partea cunoscută, segmentul roșu care reprezintă numărul n.

Pentru pasul egalarea părților este necesar să observăm din ce este formată cea de a doua cantitate.

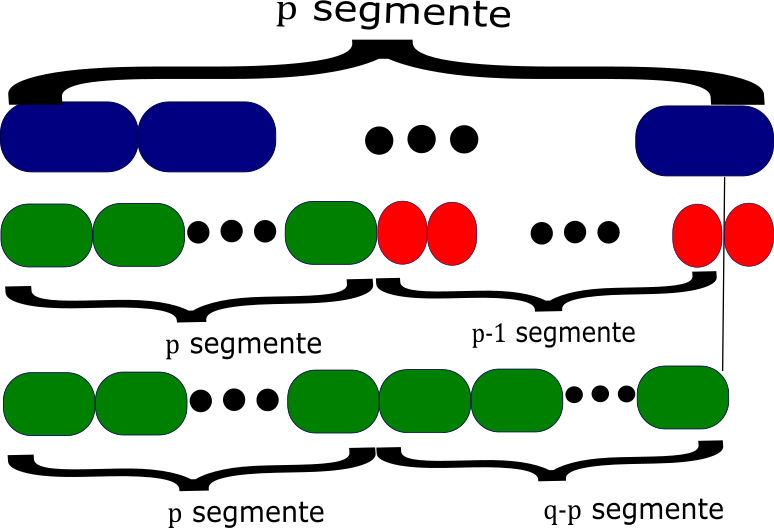
Inițial, a doua cantitate este reprezentată de cele p segmente albastre, iar la final, cele q segmente verzi reprezintă cantitatea a doua mai puțin n. Din cele p segmente albastre se pot obține p segmente verzi și p segmente roșii, deci cele q-p segmente verzi rămase sunt EGALE cu cele p-1 segmente roșii. Astfel calculul

    \[n \times \left(p-1\right) : \left(q-p\right) \]

permite determinarea cantității pe care o reprezintă un segment verde, o notăm aici cu v.

Astfel, prima cantitate, numărul mai mic, se determină prin operația

    \[ v+n,\]

iar cantitatea a două, cea mai mare, se determină prin operațiile

    \[ q \times v +n.\]

Un exemplu de problemă care poate fi rezolvată prin această metodă este Problema 1. [12, G.M. 3/1998]. În această problemă avem p=3, q=4 și n=3. Practic, cele trei persoane consumă trei ardei și trei roșii. Astfel cele trei grupe inițiale de ardei generează alte patru grupe noi, dintre care trei sunt grupe obținute din cele inițiale, iar cea de a patra grupă reprezintă 3 \times \left( 3-1\right) = 6. Deci numărul de ardei este

    \[6+3=9,\]

iar numărul de roșii este

    \[3 \times 9 = 27. \]