AM1-Curs-02

Spaţiile 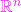\mathbb{R}^n

Se consideră notaţia

    \[\mathbb{R}^{n}=\mathbb{R} \times \mathbb{R} \times \cdots \times \mathbb{R} = \left\{x=(x_1,x_2,...,x_n):x_i\in \mathbb{R}, i=1,2,...,n\right\},\]

unde n este un număr natural nenul.

Mulţimea \mathbb{R}^n se numeşte spaţiul cu n dimensiuni, iar elementele sale le vom numi puncte.

Dacă x \in \mathbb{R}^n, atunci

    \[x= \left(x_1,x_2,\cdots , x_n\right),\]

unde numerele reale x_1, x_2, \cdots, x_n se numesc coordonatele punctului x.

Pentru elementele din \mathbb{R}^n se definesc operaţiile:

  • adunarea

        \[x+y=(x_1+y_1,x_2+y_2,\cdots,x_n+y_n), \forall x=(x_1,x_2,\cdots ,x_n)\in \mathbb{R}^n, y=(y_1,y_2,\cdots ,y_n)\in\mathbb{R}^n.\]

  • înmulţirea cu scalari

        \[\alpha\cdot x=(\alpha x_1,\alpha x_2,\cdots,\alpha x_n), \forall \alpha \in \mathbb{R}, x=(x_1,x_2,\cdots ,x_n)\in\mathbb{R}^n.\]

  • produsul scalar

        \[<x,y> = \sum\limits_{i=1}^{n}{x_i y_i},\,\ (\forall) x=(x_1,x_2,\cdots ,x_n), y=(y_1,y_2,\cdots ,y_n)\in\mathbb{R}^n\]

Observaţie. \left(\mathbb{R}^n,+,\cdot\right) este un spaţiu vectorial real. [ro], [en]

Detalii şi proprietăţi referitoare la produsul scalar pot fi găsite aici [1], [2].

Norma şi distanţa în 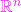\mathbb{R}^n

Fie x=(x_1,x_2,\cdots ,x_n)\in\mathbb{R}^n. Numărul nenegativ notat \left\|x\right\|, definit prin egalitatea

    \[ \left\|x\right\|=\sqrt{<x,x>}=\sqrt{\sum\limits_{i=1}^{n}{x_{i}^2 }} \]

se numeşte norma punctului x.

Observaţie. Norma mai sus menţionată se numeşte norma euclidiană. Pe mulţimea \mathbb{R}^n se pot defini mai multe norme, vezi [exemple de norme] sau [norme].

Funcţia d:\mathbb{R}^n\times\mathbb{R}^n\rightarrow \mathbb{R} definită prin

(1)   \begin{equation*} d(x,y)=\left\|x-y\right\|, \forall x,y\in \mathbb{R}^n \end{equation*}

se numeşte distanţa dintre punctele x,y\in \mathbb{R}^n.

Exemple de distanţe: distanţa Minkowski,  distanţa Chebyshev,  alte distanţe [1],  [2].

Exerciții referitoare la noțiunea de distanță și cea de spațiu metric pot fi găsite aici.

Vecinătăţi

Fie a\in\mathbb{R}^n şi r>0. Se numeşte sferă deschisă (bilă deschisă) de centru a şi rază r mulţimea

(2)   \begin{equation*} V_{r}(a) = \left\{x\in\mathbb{R}^n|\left\|x-a\right\|<r\right\}. \end{equation*}

Fie a\in\mathbb{R}^n. Se numeşte vecinătate a punctului a orice submulţime a lui \mathbb{R}^n care conţine o bilă deschisă V_r\left(a\right).

Mulţimea tuturor vecinătăţilor punctului a se notează \mathcal{V}_r(a).

Despre vecinătăţi se pot găsi infromaţii aici.

Alte elemente de topologie pot fi găsite aici.