AM2-Curs-04
Diferențiala Fréchet
Definiție. Fie ![]() o mulțime deschisă,
o mulțime deschisă, ![]() și
și ![]() o funcție. Spunem că funcția
o funcție. Spunem că funcția ![]() este diferențiabilă în sens Fréchet în punctul
este diferențiabilă în sens Fréchet în punctul ![]() (sau simplu,
(sau simplu, ![]() este diferențiabilă în punctul
este diferențiabilă în punctul ![]() ) dacă există o aplicație liniară
) dacă există o aplicație liniară ![]() astfel ca pentru orice
astfel ca pentru orice ![]() pentru care
pentru care ![]() să aibă loc relația
să aibă loc relația
(1) ![]()
unde ![]() este norma euclidiană din
este norma euclidiană din ![]() .
.
Dacă funcția ![]() este diferențiabilă în punctul
este diferențiabilă în punctul ![]() , atunci aplicația liniară
, atunci aplicația liniară ![]() se numește derivata în sens Fréchet sau derivata tare a funcției
se numește derivata în sens Fréchet sau derivata tare a funcției ![]() în punctul
în punctul ![]() și o notăm cu
și o notăm cu
![]()
Atunci pentru orice ![]() , funcția
, funcția ![]() se numește diferențiala în sens Fréchet sau diferențiala tare a funcției
se numește diferențiala în sens Fréchet sau diferențiala tare a funcției ![]() în punctul
în punctul ![]() și se notează
și se notează
![]()
Teoremă. Dacă ![]() este o mulțime deschisă,
este o mulțime deschisă, ![]() și
și ![]() este diferențiabilă în sens Fréchet în
este diferențiabilă în sens Fréchet în ![]() , atunci diferențiala în sens Fréchet a funcției
, atunci diferențiala în sens Fréchet a funcției ![]() în punctul
în punctul ![]() este unică.
este unică.
Teoremă. O funcție diferențiabilă Fréchet într-un punct este continuă în acel punct.
Teoremă. Dacă ![]() este deschisă,
este deschisă, ![]() și
și ![]() este diferențiabilă în
este diferențiabilă în ![]() , atunci diferențiala Fréchet a lui
, atunci diferențiala Fréchet a lui ![]() în
în ![]() are expresia
are expresia
(2) 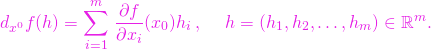
Teoremă. Fie ![]() este o mulțime deschisă,
este o mulțime deschisă, ![]() . Dacă funcția
. Dacă funcția ![]() este diferențiabilă în sens Fréchet în
este diferențiabilă în sens Fréchet în ![]() , atunci există
, atunci există ![]() și funcția
și funcția ![]() continuă în punctul
continuă în punctul ![]() pentru care
pentru care ![]() și
și
![]()
O aplicație a acestui rezultat se pate găsi în următorul Exemplu.

Comentarii recente