AM2-Curs-05-b

Optim cu legături

În unele probleme practice se cere determinarea punctelor de optim (extrem) local ale unei funcții reale de variabilă vectorială, în condițiile în care variabila vectorială este supusă unor restricții, adică trebuie să satisfacă anumite condiții particulare. O asemenea problemă se numește problemă de optim (extrem) condiționat sau optim cu legături.

Fie D\subset\mathbb{R}^n o mulțime deschisă, k<n un număr natural și funcția

    \[f:D\to\mathbb{R}, f\left(x\right)=f\left(x_1,x_2,\dots,x_n\right), \forall \;x=\left(x_1,x_2,\dots,x_n\right)\in D.\]

Fie de asemenea ecuațiile

(1)   \begin{equation*} \left\{\begin{array}{ll} F_1\left(x_1,x_2,\dots,x_n\right) &=0,\\[5pt] F_2\left(x_1,x_2,\dots,x_n\right) & =0,\\[5pt] ~~~\cdot~~~\cdot~~~\cdot~~~\cdot~~~\cdot &\\[5pt] F_k\left(x_1,x_2,\dots,x_n\right) &=0, \end{array}\right. \end{equation*}

unde F=\left(F_1,F_2,\dots,F_k\right):D\to\mathbb{R}^k, cu componentele F_i:D\to\mathbb{R}, i=\overline{1,k},  care sunt numite legături – sau condițiile de legătură – dintre variabilele reale x_1,x_2,\dots,x_n.

Notăm cu 

    \[M=\{x\in D:F_i(x)=0,\;i=1,2,\dots,k,\;x=(x_1,x_2,\dots, x_n)\in D\}\]

mulțimea tuturor punctelor din D care verifică ecuațiile (1). Spunem că punctul x^0\in M este un punct de minim (maxim) local condiționat – sau minim (maxim) local cu legături – al funcției f, dacă există V\in\mathcal{V}(x^0),\;V\subset M, astfel încât

    \[f(x)\geq f(x^0)\quad(\text{respectiv}\quad f(x)\leq f(x^0)),\;\forall \;x\in V.\]

Cu alte cuvinte x^0 este un punct de extrem local condiționat dacă x^0 este un punct de extrem local al funcției f și x^0\in M.

Aplicația L:D\times\mathbb{R}^k\to\mathbb{R}, defintă prin

    \[ L(x,\lambda)=f(x)+\lambda_1 F_1(x)+\lambda_2 F_2(x)+ \cdots +\lambda_k F_k(x)\,, \]

pentru orice x=(x_1,x_2,\dots,x_n)\in D și orice \lambda=\left(\lambda_1,\lambda_2,\dots,\lambda_k\right)\in\mathbb{R}^k se numește funcția lui Lagrange. Numerele \lambda_1, \lambda_2, \dots,\lambda_k poartă numele de multiplicatorii lui Lagrange.

Condiții suficiente de optim condiționat

Fie D\subset\mathbb{R}^m o mulțime deschisă, f,F_1,F_2,\dots,F_k:D\to\mathbb{R} funcții de clasă C^2 într-o vecinătate a lui x^0\in D și fie (x^0,\lambda^0), unde x^0=(x_1^0,x_2^0,\dots,x_m^0)\in M\subset D și \lambda^0=(\lambda_1^0,\lambda_2^0,\dots,\lambda_k^0)\in\mathbb{R}^k, un punct critic al lagrangeanului

    \[ L(x,\lambda)=f(x)+\sum\limits^k_{i=1}\lambda_i F_i(x),\; x\in D,\;\lambda\in\mathbb{R}^k. \]

Fie L_0:D\to\mathbb{R}, definită pentru orice x\in D prin

    \[ L_0(x):=L(x,\lambda^0)=f(x)+\lambda^0_1 F_1(x)+ \lambda_2^0 F_2(x)+\cdots +\lambda_k^0 F_k(x)\,, \]

obținută din lagrangean pentru \lambda=\lambda^0=(\lambda_1^0,\lambda_2^0,\dots,\lambda_k^0) și diferențiala sa de ordinul doi în x^0,

    \[d_{x^0}^2 L_0(h)=\sum\limits^m_{i,j=1}\frac{\partial^2 L_0} {\partial x_i\,\partial x_j}\,(x^0)h_i\,h_j,\quad h=(h_1,h_2,\dots,h_m)\in\mathbb{R}^m\]

Dacă în această diferențială se înlocuiesc h_1,h_2,\dots,h_k prin expresiile lor liniare, în funcție de h_{k+1}, h_{k+2},\dots,h_m, obținute din sistemul liniar

    \[ \left\{\begin{array}{ll} \frac{\partial F_1}{\partial x_1}\,(x^0)h_1+ \frac{\partial F_1}{\partial x_2}\,(x^0) h_2+ \cdots +\frac{\partial F_1}{\partial x_k}\,(x^0)h_k +\cdots +\frac{\partial F_1}{\partial x_m}\,(x^0)h_m &=0,\\[12pt] \frac{\partial F_2}{\partial x_1}\,(x^0)h_1+ \frac{\partial F_2}{\partial x_2}\,(x^0)h_2 + \cdots +\frac{\partial F_2}{\partial x_k}\,(x^0)h_k+ \cdots +\frac{\partial F_2}{\partial x_m}\,(x^0)h_m &=0,\\[5pt] ~~~\cdot~~~\cdot~~~\cdot~~~\cdot~~~\cdot~~~\cdot~~~\cdot~~~\cdot ~~~\cdot~~~\cdot~~~\cdot~~~\cdot~~~\cdot~~~\cdot~~~\cdot~~~\cdot&\\[5pt] \frac{\partial F_k}{\partial x_1}\,(x^0)h_1+ \frac{\partial F_k}{\partial x_2}\,(x^0)h_2+ \cdots +\frac{\partial F_k}{\partial x_k}\,(x^0)h_k+ \cdots+\frac{\partial F_k}{\partial x_m}\,(x^0)h_m &=0, \end{array}\right.\]

atunci se obține o formă pătratică

    \[P(h_{k+1},h_{k+2},\dots,h_m)\]

în variabilele h_{k+1},\dots,h_m și sunt adevărate afirmațiile:

  • dacă forma pătratică 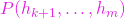P(h_{k+1},\dots,h_m) este pozitiv definită, atunci rezultă că punctul 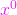x^0 este un punct de minim condiționat al funcției f;
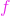  • dacă forma pătratică 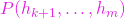P(h_{k+1},\dots,h_m) este negativ definită, atunci rezultă că 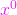x^0 este un punct de maxim condiționat al funcției f.

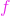Exemplul 1

Să se determine punctele de pe sfera 

    \[x^2+y^2+z^2=9\]

 în care funcția f:\mathbb{R}^3\to\mathbb{R} definită prin 

    \[f(x,y,z)=x-2y+2z\]

 ia valori extreme.

Observație: Cerința problemei poate  fi interpretată ca determinarea punctelor de intersecție dintre sfera x^2+y^2+z^2=9 și planul x-2y+2z=0, puncte care sunt așezate cel mai jos, respectiv cel mai sus, pe sferă.

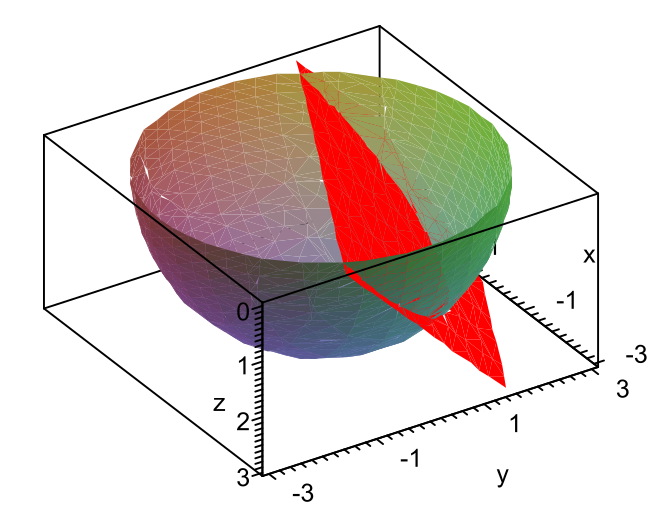
Soluția este aiciextrem_legaturi