AM2-Curs-10

Integrarea funcțiilor raționale

Fie f: D \to \mathbb{R} cu

    \[f\left(x\right) = \frac{P\left(x\right)}{Q\left(x\right)},\]

unde mulțimea D\subset \mathbb{R} este astfel încât funcția f să fie bine definită și să admită primitive pe D.

Integrarea funcțiilor raționale are la bază integrarea funcțiilor raționale simple.

Relativ la primitivele funcțiilor simple, au loc următoarele egalități

(1)   \begin{equation*} \int \frac{A}{x-a}\, dx=A\cdot\ln \,\,\left| {\,x-a\,}\right| +\mathcal{C}, \end{equation*}

(2)   \begin{equation*} \int \frac{A}{(x-a)^{n}}\,d\,x=A\cdot \int (x-a)^{-n}\,d\,x=A\cdot \frac{% (x-a)^{-n+1}}{-n+1}+\mathcal{C}=\frac{A}{1-n}\,\,\,\frac{1}{(x-a)^{n-1}}+\mathcal{C}. \end{equation*}

Pentru determinarea primitivei unei funcții definită prin

(3)   \begin{equation*} f(x)=\frac{Ax+B}{(ax^{2}+bx+c)^{n}},\,\,x\in I\subset D\,,\,\,\,\Delta =b^{2}-4ac<0, \end{equation*}

se va ține cont de forma canonică

    \[ ax^{2}+bx+c=a\,\left[ {\,\left( {x+\frac{b}{2a}}\right) ^{2}-\frac{\Delta }{% 4a^{2}}\,}\right] =a\,\left[ {\,\left( {x+\frac{b}{2a}}\right) ^{2}+\alpha ^{2}}\right], \]

unde \alpha =\frac{\sqrt{-\Delta }}{2a}\in \mathbb{R}. Cu ajutorul substituției

    \[x+\dfrac{b}{2a}:=t\]

se obține

(4)   \begin{equation*} \int \frac{A\left( {t-\dfrac{b}{2a}}\right) +B}{a^{n}(t^{2}+\alpha ^{2})^{n}}% \,dt=\frac{A}{a^{n}}\,\int \,\frac{t}{(t^{2}+\alpha ^{2})^{n}}\,dt+\frac{1}{% a^{n}}\left( {B-\frac{Ab}{2a}}\right) \,\int \frac{1}{(t^{2}+\alpha ^{2})^{n}% }\,dt. \end{equation*}

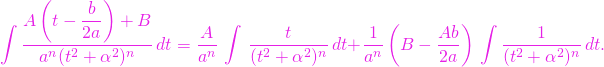
Egalitatea de mai sus (4) reduce calculul primitivei funcției (3) la determinarea primitivelor

(5)   \begin{equation*} \int \frac{t}{(t^{2}+\alpha ^{2})^{n}}\,d\,t \end{equation*}

(6)   \begin{equation*} \int \frac{1}{(t^{2}+\alpha ^{2})^{n}}\,d\,t, \end{equation*}

unde n \in \mathbb{N}^\ast. Pentru aceste primitive, au loc următoarele egalități

(7)   \begin{equation*}\int\frac{t}{t^2+\alpha^2}\,dt = \frac{1}{2}\,\ln \,(t^{2}+\alpha ^{2})+\mathcal{C}\,,\,\,t\in \mathbb{R}\end{equation*}

(8)   \begin{equation*}\int \frac{1}{t^{2}+\alpha ^{2}}\,d\,t=\frac{1}{\alpha }\arctg\,\,\frac{t}{\alpha }+\mathcal{C},\,\,\,\,t{\in }\mathbb{R}\end{equation*}

(9)   \begin{equation*} \int \frac{t}{(t^{2}+\alpha ^{2})^{n}}\,dt=\frac{1}{2(1-n)}\,\,\,\frac{1}{(t^{2}+\alpha ^{2})^{n-1}}+\mathcal{C},\,\,\,\,t\in \mathbb{R}.\end{equation*}

Dacă notăm

    \[I_{n}:=\int {\dfrac{dt}{(t^{2}+\alpha ^{2})^{n}}},\]

atunci are loc relația de recurență

(10)   \begin{equation*} I_{n}=\frac{1}{\alpha ^{2}}\,\left[ {\frac{t}{2(n-1)(t^{2}+\alpha ^{2})^{n-1}% }+\frac{2n-3}{2n-2}I_{n-1}\,}\right] , n\ge 2 \end{equation*}

cu

    \[ I_{1}=\int \frac{1}{t^{2}+\alpha ^{2}}\,d\,t=\frac{1}{\alpha }\,\arctg\,\,% \frac{t}{\alpha }+C\,,\,\,\,\,\,t\in \mathbb{R}. \]

O listă cu primitive poate fi consultată aici.

Un exemplu de determinare a primitivei unei funcții raționale poate fi consultat aici.