AM2-Curs-12
Integrale iraționale
Aici vor fi prezentate substituțiile lui Euler utile la determinarea primitivelor unor funcții iraționale prin reducerea la integrale raționale. Mai exact, vom considera integralele de forma
(1) 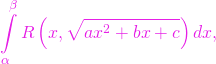
unde ![]() este o funcție rațională în două variabile.
este o funcție rațională în două variabile.
Integrala (1) se reduce întotdeauna la o integrală rațională dacă următoarele condiții sunt satisfăcute:
a) ![]() , oricare ar fi
, oricare ar fi ![]() ;
;
b) ![]() , pentru orice
, pentru orice ![]() ;
;
c) ![]() și
și ![]() .
.
Reducerea unei integrale de forma (1) la o integrală rațională se poate realiza prin intermediul schimbărilor de
variabile ale lui Euler.
Cazul 1
Dacă ![]() se poate face schimbarea de variabilă
se poate face schimbarea de variabilă
(2) ![]()
care implică
![]()
Deoarece ![]() este o funcție continuă în variabila
este o funcție continuă în variabila ![]() , dacă
, dacă ![]() parcurge intervalul
parcurge intervalul ![]() , atunci
, atunci ![]() parcurge intervalul
parcurge intervalul ![]() , unde
, unde ![]() și
și ![]() se obțin din (2) pentru
se obțin din (2) pentru ![]() , respectiv
, respectiv ![]() .
.
Atunci integrala (1) devine
![Rendered by QuickLaTeX.com \[ \int\limits_{t_{1}}^{t_{2}}{R(u(t),t-\sqrt{a}\cdot u(t))\cdot {u}^{\prime }(t)dt}=\int\limits_{t_{1}}^{t_{2}}{R_{1}(t)dt}, \]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-217b6c5dd9fb2c0219fc01d4301ad881_l3.png)
unde ![]() este o funcție rațională în variabila
este o funcție rațională în variabila ![]() .
.
Cazul 2
Dacă ![]() se poate face schimbarea de variabilă
se poate face schimbarea de variabilă
(3) ![]()
Se exprimă ![]() în funcție de
în funcție de ![]() și se obține
și se obține
![]()
cu ![]() . Integrala (1) devine
. Integrala (1) devine
![Rendered by QuickLaTeX.com \[ \int\limits_{t_{1}}^{t_{2}}{R(u(t),tu(t)+\sqrt{c}){u}^{\prime }(t)dt}=\int\limits_{t_{1}}^{t_{2}}{R_{2}(t)dt}, \]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-274a3f769303a2067a4b4e505676fd00_l3.png)
unde ![]() este o funcție rațională în variabila
este o funcție rațională în variabila ![]() .
.
Cazul 3
Dacă ![]() , adică trinomul de gradul doi
, adică trinomul de gradul doi ![]() are rădăcinile reale și distincte
are rădăcinile reale și distincte ![]() .
.
Se poate face una din schimbările de variabilă
(4) ![]()
sau
(5) ![]()
De aici se obține
![]()
și
![]()
Integrala (1) devine
![Rendered by QuickLaTeX.com \[\int\limits_{t_{1}}^{t_{2}}{R\left( u(t),\dfrac{a(x_{1}-x_{2})t}{t^{2}-a}\right) }u^{\prime }(t)dt=\int\limits_{t_{1}}^{t_{2}}{R_{3}(t)dt},\]](https://hmandrei.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-a9975b8d1b01c387fc2013c8ad73ba97_l3.png)
unde ![]() este o funcție rațională în variabila
este o funcție rațională în variabila ![]() .
.
O listă cu integralele iraționale poate fi consultată aici.
Un exemplu pentru determinarea primitivei unei funcții iraționale poate fi găsit aici.

Comentarii recente